Development Status
- 5 - Production/Stable
Environment
- Console
Framework
- IPython
- Jupyter
Intended Audience
- Education
- Other Audience
- Science/Research
Operating System
- OS Independent
Programming Language
- Python :: 2.7
- Python :: 3
Topic
- Scientific/Engineering
- Scientific/Engineering :: Artificial Intelligence
- Scientific/Engineering :: Mathematics
A stochastic numerical optimization algorithm for difficult (non-convex, ill-conditioned, multi-modal, rugged, noisy) optimization problems in continuous or mixed-integer search spaces, implemented in Python.
Typical domain of application are unconstrained or bound-constrained objective functions with:
search space dimension between, say, five and a few hundred,
no gradients available,
at least, say, 100 times dimension function evaluations needed to get satisfactory solutions,
non-separable, ill-conditioned, or rugged/multi-modal landscapes.
Nonlinear constraints handling is available too. The CMA-ES is quite reliable, however for small budgets (fewer function evaluations than, say, 100 times dimension) or in very small dimensions faster methods are available.
The pycma module provides two independent implementations of the CMA-ES algorithm in the classes cma.CMAEvolutionStrategy and cma.purecma.CMAES.
Installation
In the terminal command line type
python -m pip install cma
The package will be downloaded and installed automatically. To upgrade an existing installation, ‘install’ must be replaced by ‘install -U’. For the documentation of pip, see here.
Alternatively, download and unpack the cma-...tar.gz file under the above Download files link. The folder cma from the tar archive can be used without any installation (for import to find it, it must be in the current folder or the Python search paths) or can be installed by pip install -e ..
Usage Example
In a Python shell:
>>> import cma
>>> help(cma)
<output omitted>
>>> es = cma.CMAEvolutionStrategy(8 * [0], 0.5)
(5_w,10)-aCMA-ES (mu_w=3.2,w_1=45%) in dimension 8 (seed=468976, Tue May 6 19:14:06 2014)
>>> help(es) # the same as help(cma.CMAEvolutionStrategy)
<output omitted>
>>> es.optimize(cma.ff.rosen)
Iterat #Fevals function value axis ratio sigma minstd maxstd min:sec
1 10 1.042661803766204e+02 1.0e+00 4.50e-01 4e-01 5e-01 0:0.0
2 20 7.322331708590002e+01 1.2e+00 3.89e-01 4e-01 4e-01 0:0.0
3 30 6.048150359372417e+01 1.2e+00 3.47e-01 3e-01 3e-01 0:0.0
100 1000 3.165939452385367e+00 1.1e+01 7.08e-02 2e-02 7e-02 0:0.2
200 2000 4.157333035296804e-01 1.9e+01 8.10e-02 9e-03 5e-02 0:0.4
300 3000 2.413696640005903e-04 4.3e+01 9.57e-03 3e-04 7e-03 0:0.5
400 4000 1.271582136805314e-11 7.6e+01 9.70e-06 8e-08 3e-06 0:0.7
439 4390 1.062554035878040e-14 9.4e+01 5.31e-07 3e-09 8e-08 0:0.8
>>> es.result_pretty() # pretty print result
termination on tolfun=1e-11
final/bestever f-value = 3.729752e-15 3.729752e-15
mean solution: [ 1. 1. 1. 1. 0.99999999 0.99999998
0.99999995 0.99999991]
std deviation: [ 2.84303359e-09 2.74700402e-09 3.28154576e-09 5.92961588e-09
1.07700123e-08 2.12590385e-08 4.09374304e-08 8.16649754e-08]optimizes the 8-dimensional Rosenbrock function with initial solution all zeros and initial sigma = 0.5.
Pretty much the same can be achieved with the “one-liner”
>>> import cma
>>> xopt, es = cma.fmin2(cma.ff.rosen, 8 * [0], 0.5)
<output omitted>where cma.fmin2 provides also options for restarts.
The same can be run via the ask-and-tell interface which gives the user direct control over the iteration loop of the algorithm:
>>> import cma
>>> es = cma.CMAEvolutionStrategy(12 * [0], 0.5)
>>> while not es.stop():
... solutions = es.ask()
... es.tell(solutions, [cma.ff.rosen(x) for x in solutions])
... es.logger.add() # write data to disc to be plotted
... es.disp()
<output omitted>
>>> es.result_pretty()
<output omitted>
>>> cma.plot() # shortcut for es.logger.plot()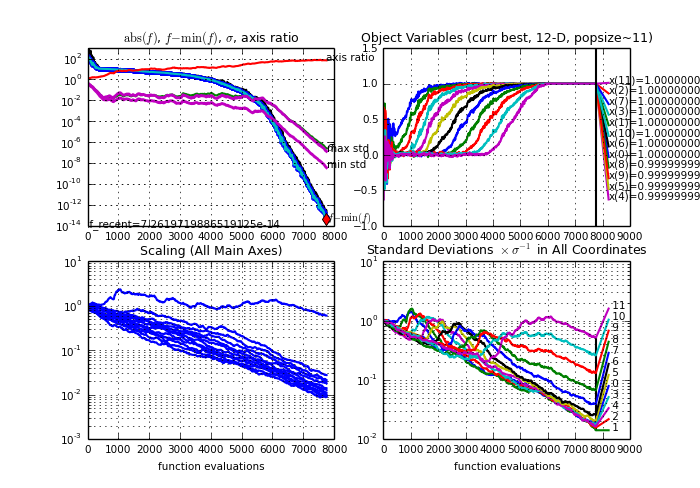
A single run on the 12-dimensional Rosenbrock function.
The CMAOptions class manages the options for CMAEvolutionStrategy. The options class allows for substring search. For example, verbosity options can be found like
>>> import cma
>>> cma.s.pprint(cma.CMAOptions('erb'))
{'verb_log': '1 #v verbosity: write data to files every verb_log iteration, writing can be time critical on fast to evaluate functions'
'verbose': '1 #v verbosity e.v. of initial/final message, -1 is very quiet, not yet implemented'
'verb_plot': '0 #v in fmin(): plot() is called every verb_plot iteration'
'verb_disp': '100 #v verbosity: display console output every verb_disp iteration'
'verb_filenameprefix': 'outcmaes # output filenames prefix'
'verb_append': '0 # initial evaluation counter, if append, do not overwrite output files'
'verb_time': 'True #v output timings on console'}Options are passed as another argument, after sigma, to cma.fmin2 or cma.CMAEvolutionStrategy like
>>> import cma
>>> es = cma.CMAEvolutionStrategy(8 * [0], 0.5,
{'verb_disp': 1}) # display each iterationDocumentations
The full package API documentation:
See also
An FAQ (under development)
General CMA-ES source code page with practical hints
Dependencies
required (unless for cma.purecma): numpy – array processing for numbers, strings, records, and objects
optional (highly recommended): matplotlib – Python plotting package (includes pylab)
Use pip install numpy etc. for installation. The cma.purecma submodule can be used without any dependencies installed.
License: BSD-3-Clause
